백준 2225번 : 합분해 [자바]

 

🧫 문제 분석

 

✔️ 출처

합분해 골드 5

 

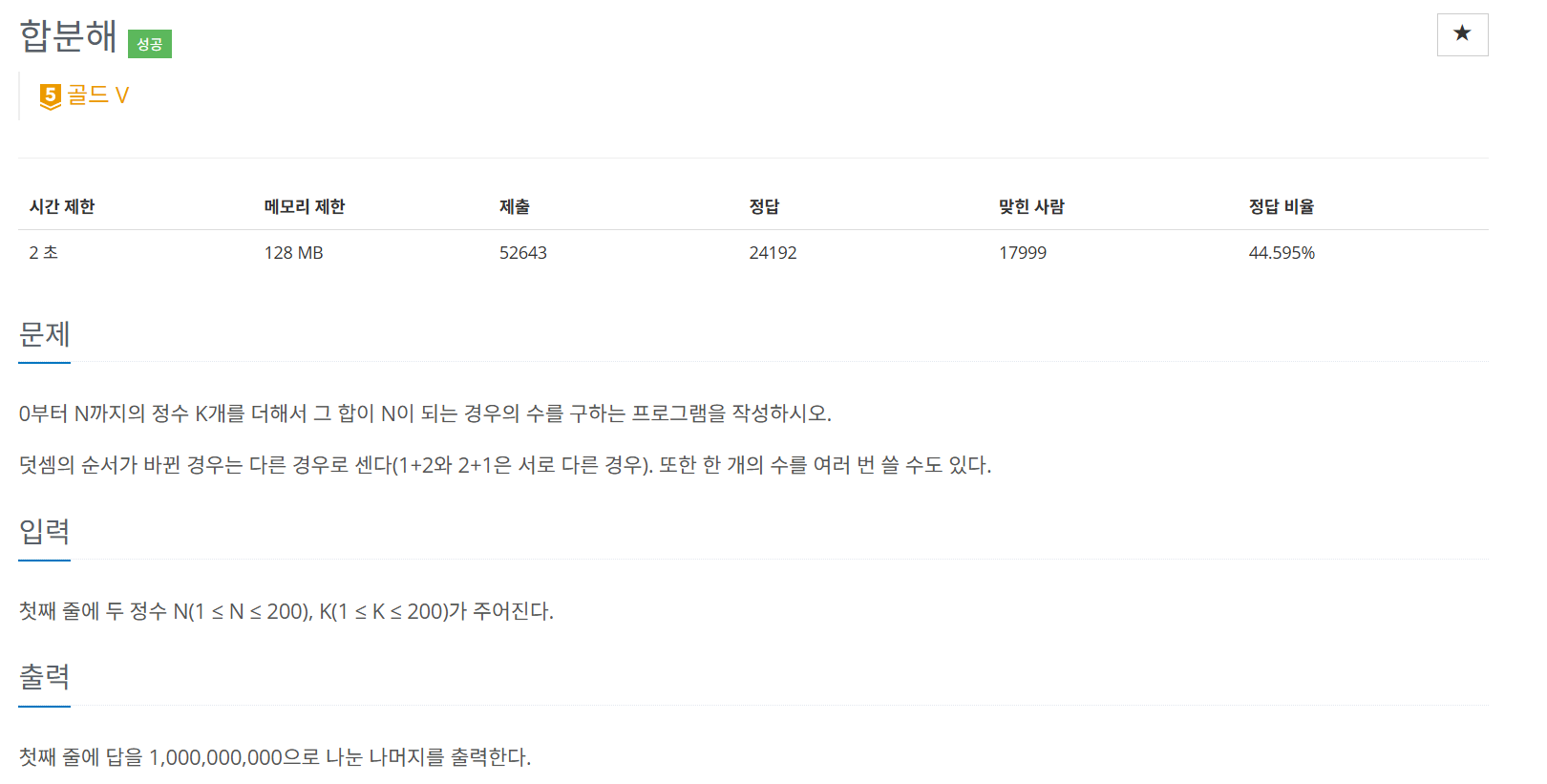
📖 문제

 

DP 연습셋 문제중 하나

 

0~N까지의 정수 K개를 더한 합이 N이 되는 경우의 수 구하기

 

0~N까지의 수(i) 를 1~K개를 뽑아서 더해 i가 되는 경우의 수를 구하는 식으로 구해봤더니 맞았다.

i  \ k	1	2	3	4
0	1	1	1	1
1	1	2	3	4
2	1	3	6	10
3	1	4	10	20
4	1	5	15	35
5	1	6	21	56
6	1	7	28	84

 

구한 결과

점화식이 나왔다.

DP[N][k] = (DP[N-1][k] + DP[N][k-1]) % 1000000000;

 

 

그리고 중요한 점은 문제에서 출력시 % 10억을 하라는 조건이 있으므로 잘 확인하자.

---

🔅 문제 풀이

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
    static final int MOD = 1000000000;
    
    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int n = Integer.parseInt(st.nextToken());
        int k = Integer.parseInt(st.nextToken());

        int[][] dp = new int[n + 1][k + 1];

        // 0을 k개로 만드는 경우의 수는 모두 1
        for (int i = 1; i <= k; i++) {
            dp[0][i] = 1;
        }

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= k; j++) {
                dp[i][j] = (dp[i - 1][j] + dp[i][j - 1]) % MOD;
            }
        }

        System.out.println(dp[n][k]);
    }
}

 

 

 

❗ 오답노트 / 필요한 지식

1.  풀이 성공!