요격 시스템 [자바]

🧫 문제 분석
✔️ 출처
📖 문제
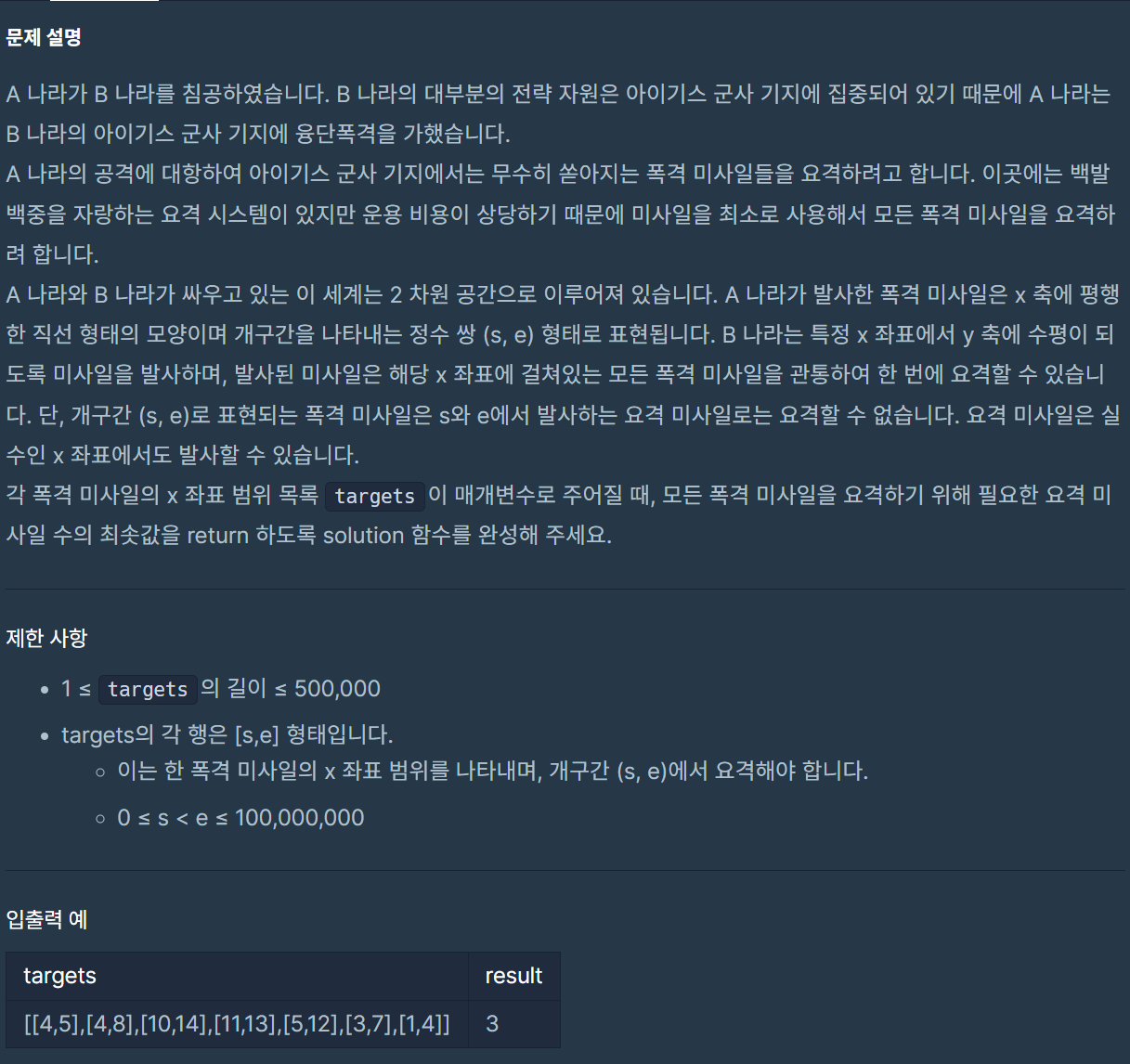

핵심은 A 나라의 폭격 미사일을 모두 요격하면서, 요격 미사일 개수가 최소가 되게하는 것이다.
최소한의 비용으로 최대한의 효율 즉, 탐욕법이라고 볼 수 있다.
또한 요격 미사일은 개구간 (s, e)에서 s, e위치에서 요격 미사일로 요격 불가능하다.
제한사항을 보면 0부터 1억까지 s와 e가 분포되어있기에 단순히 미사일이 지나간 좌표를 배열로 만들어서 카운트하는 것은 불가능하다는 것을 알 것이다.
그렇다면 참고해볼 것은 targets의 길이가 50만이라는 점이다.
뭔가 배열 정렬, 혹은 탐색 등으로 문제 풀이를 생각해보는 것이다.
필자는 고민해보다가 A나라의 폭격 미사일들을 s(시작 좌표)로 정렬
그리고 하나의 폭격 미사일의 범위에 대해서 다른 미사일들과 비교하여 (s, e)구간 즉, 동시 요격 가능 공간이 있는지 탐색하였다.
중요
탐색할 때 먼저 기준 미사일의 e값을 cutLine저장하고, cutLine을 기준으로 같이 요격가능한 미사일들을 탐색하되 여기서 요격 가능한 미사일의 e값과 비교하여 최솟값을 cutline으로 설정한다.
그 이유는 이 예시를 보면 알 수 있다.
입력 : [[4, 5], [4, 8], [10, 14], [11, 13], [5, 12], [3, 7], [1, 4], [10, 11]]
리턴 : 4

위 빨간색이 추가되었다 했을 때
cutLine 최솟값 갱신을 하지 않을 경우
[5,12] 의 12가 계속 유지되면서 원래는 [10,11], [10,14]만 같이 요격되어야하고 [11,12] 가 한 번 더 따로 요격되어야하는데
cutLine이 12로 유지로 12 미만에 있는 [10,11], [10, 14], [11,13] 이 요격된다는 잘못된 오류가 발생한다.
🔅 문제 풀이
import java.util.Arrays;
class Solution {
// 2차원
// A 공격 : x 축 평행 직선 형태 정수 쌍(s,e) 형태
// B: 특정 x 좌표에서 y축에 수평 발사, 관통 (s, e) 인 s, e 는 요격 불가
// 요격 미사일은 실수인 x좌표에서도 발사 가능
// 문제 : 모든 폭격 미사일을 요격하기 위해 필요한 요격 미사일 수의 최솟값
public int solution(int[][] targets) {
boolean[] check = new boolean[targets.length]; // 미사일 요격 여부
int answer = 0;
// s 기준으로 오름차순 정렬
Arrays.sort(targets, (o1, o2) -> o1[0] - o2[0]);
for (int i = 0; i < targets.length; i++) {
// 요격당했다면 다음 미사일로
if (check[i]) continue;
// 미사일의 e의 값 저장
int cutLine = targets[i][1];
// 요격할 미사일들 선택
for (int j = i + 1; j < targets.length; j++) {
if (cutLine > targets[j][0]) {
// 요격 가능 미사일의 e값과 현재 cutLine 값중 최솟값을 가짐
cutLine = Math.min(cutLine, targets[j][1]);
check[j] = true;
}else {
break;
}
}
answer++;
}
return answer;
}
}
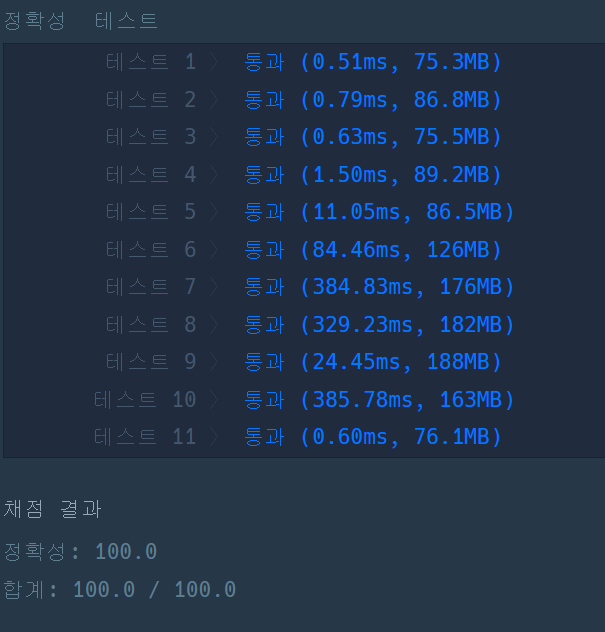
❗ 오답노트 / 필요한 지식
- 예외를 금방 찾아서 다행이다.
- 항상 예외, 특수 케이스를 잘 찾자.